AMR Newsletter February 2024
Fundraising Update
2024 promises to be an exciting year for the Association for Mathematical Research. Thanks to a generous donation endowing the Fred R. Cohen Prize, contributions from many of our members, and a major year-end gift, the AMR raised over $500,000 in 2023. This funding will allow us to support new Diamond Open Access journals, create mathematical videos and pursue other projects. Look for further announcements during the year. Below is information about current and ongoing projects. |
AMR Members Meeting
We are planning the first general meeting of AMR members, on April 11, 2024, at 9:00 AM (Los Angeles), 12:00 PM (New York), 5:00 PM (London) 6:00 PM (Paris) 7:00 PM (Tel-Aviv). The meeting will take place on Zoom. You’ll hear about projects underway and projects proposed. There will be a discussion on setting AMR priorities for the coming year. An invitation with a zoom link will be sent to all members shortly before the meeting. Please join us!
Journals

In 2024 we plan to add three new journals, in addition to our current pair, the Journal of the AMR (JAMR) and the Journal of Experimental Mathematics (JXM). The first of these, currently in the advanced planning stage, is the Journal of Open Mathematical Problems, or JOMP. As with our existing journals, JAMR and JXM, JOMP will be available online as a Diamond Open Access journal, with no charges to authors, libraries or readers. JOMP will feature surveys focused on major open problems. Each article will give the history of a problem, explain its importance, and discuss approaches to a solution.

Books
The third book in the AMR Research Monographs Series, JSJ Decompositions of Poincaré Duality Pairs, by Lawrence Reeves, Peter Scott and Gadde A. Swarup, is now available.

About the Book: Poincaré Duality groups and pairs have been studied by several authors since their introduction by Bieri, Johnson, Wall and others in the early 1970s. Their relations to group theory, as well as to manifold theory, were discussed by Mike Davis in a survey article which appeared in 2000. These notes continue the study of Poincare Duality Groups and pairs in a different direction. The authors show that the algebraic analogues of the Jaco-Shalen-Johannson Decomposition hold for Poincare Duality Pairs. Specialising to three dimensions, they further show that the components of the characteristic submanifold are the same as in the three manifold case and also prove an analogue of Johannson’s Deformation Theorem for Poincare Duality Pairs in dimension three. It is known from the work of B. Eckmann, Muller and Linnell that in dimension two, Poincare Duality groups are the same as surface groups. The results in these notes and results of Kapovich and Kleiner on Coarse Alexander Duality provide some steps towards a similar result in three dimensions. |
About the Authors: Lawrence Reeves is at the University of Melbourne, and was previously at Aix-Marseille University. Anandaswarup Gadde has worked in several universities, mainly TFR Mumbai and the University of Melbourne, from where he retired in 2005. Peter Scott worked at the University of Michigan in Anne Arbor, after previously working at the University of Liverpool.
All AMR books are freely available online. We welcome submissions to each of the AMR book series, the Research Monographs and the Monographs for the Profession. See the AMR Books web page for more information. |
Fred R. Cohen Prize
In the December 2023 newsletter we announced the Fred R. Cohen Prize, directed towards outstanding contributions in Algebraic Topology. The first prize will be awarded in 2024. For updates and information on the prize, please see the Fred R. Cohen Prize page on our website.
Lecture Series
Vinberg Distinguished Lecture Series
The next Vinberg Distinguished Lecture will be given by Richard Borcherds of UC Berkeley, on February 26, 2024, at 8:00 AM (Los Angeles), 11:00 AM (Toronto, New York), 5:00 PM (Zurich, Paris) 6:00 PM (Tel-Aviv).
Title: Vinberg’s Algorithm and Kac-Moody algebras.
Abstract: Vinberg’s algorithm was introduced by Vinberg in order to calculate the fundamental domains of hyperbolic reflection groups, especially those coming from Lorentzian lattices. We will show how to use it to calculate the automorphism groups of some lattices, culminating in Conway’s spectacular discovery that the Dynkin diagram of the 26-dimensional even unimodular Lorentzian lattice is the Leech lattice. We will then discuss some of the Kac-Moody algebras associated with Vinberg’s Dynkin diagrams.
About the speaker: “In 1992 Borcherds was one of the first recipients of the EMS prizes awarded at the first European Congress of Mathematics in Paris, and in 1994 he was an invited speaker at the International Congress of Mathematicians in Zurich. In 1994, he was elected to be a Fellow of the Royal Society. In 1998 at the 23rd International Congress of Mathematicians in Berlin, Germany he received the Fields Medal together with Maxim Kontsevich, William Timothy Gowers and Curtis T. McMullen. The award cited him “for his contributions to algebra, the theory of automorphic forms, and mathematical physics, including the introduction of vertex algebras and Borcherds’ Lie algebras, the proof of the Conway-Norton moonshine conjecture[14] and the discovery of a new class of automorphic infinite products. In 2012 he became a fellow of the American Mathematical Society, and in 2014 he was elected to the National Academy of Sciences.” (From Wikipedia)
AMR-RMA Recent Mathematical Advances Distinguished Lecture Series
Anton Zorich, Distinguished Professor at the Institut Mathématique de Jussieu, will give the next AMR-RMA Recent Mathematical Advances Distinguished Lecture on April 9, 2024, at 9:00 AM (Los Angeles), 12:00 PM (Montreal, New York), 5:00 PM (London) 6:00 PM (Madrid, Paris) 7:00 PM (Tel-Aviv).
Title: Random square-tiled surfaces and random multicurves in large genus. (after joint works with V. Delecroix, E. Goujard and P. Zograf)
Abstract: We will start with a count of metric integer ribbon graphs (after Kontsevich and Norbury). The answer is expressed in terms of Witten-Kontsevich correlators, which will be introduced in the talk (and which should not scare the audience in advance). Having counted ribbon graphs, we will count square-tiled surfaces. In this way we will secretly count Masur-Veech volume of the moduli space of quadratic differentials, but this would, mostly remain as a secret. We will move to Mirzakhani’s count of simple closed geodesics on hyperbolic surfaces. At first glance, it might seem unrelated to the previous count. We will see, however, that the two counts are equivalent. We will proceed with a description of random geodesic multicurves and of random square-tiled surfaces in large genus. We will conclude with a universal asymptotic formula for the Witten-Kontsevich correlators predicted by Delecroix, Goujard, Zograf and myself and recently proved by Amol Aggarwal. I will do my best to make the talk self-contained and accessible to everybody.

About the Speaker
Anton Zorich, Distinguished Professor at the Institut Mathématique de Jussieu, has made major contributions to the exploration of the moduli space of Riemann surfaces from the geometric, topological, and dynamical perspectives. Zorich’s honors include an invited talk at the ICM 2006, senior membership at the Institut Universitaire de France (2011–2016), and a Chern visiting professorship at MSRI, Berkeley (2019). Zorich’s discoveries, including the Kontsevich-Zorich cocycle, were discussed at the Bourbaki seminar in 2003 and 2012. |
Reviews
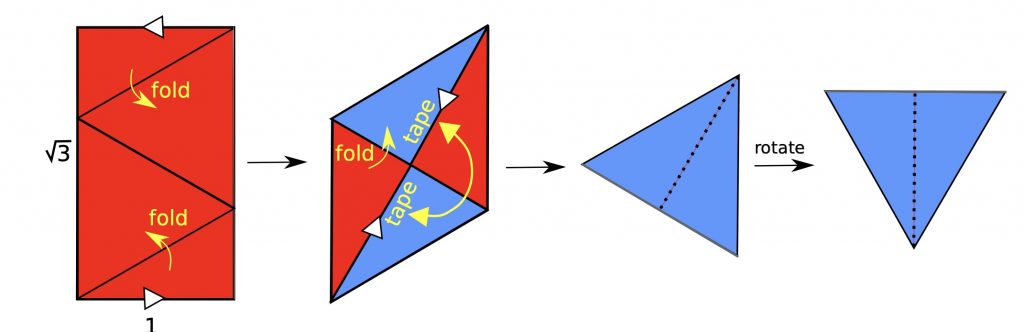
The AMR hosts reviews of classic and new mathematical results. Currently posted reviews serve as a proof-of-concept. To make this project a success we need your help! We invite AMR members to submit reviews of exciting and important results, new or classic, in any area of mathematics; please email Sergei Tabachnikov, sot2@psu.edu for more information. The reviews should be relatively short, reader-friendly and, when appropriate, well illustrated.
Volunteer
Your participation in existing and future AMR efforts to advance research and scholarship in the Mathematical Sciences is very valuable to the future of our community. Please write to AMR President Joel Hass or to any other AMR Board member expressing your interest in existing activities and/or suggesting new activities which AMR might undertake.
Membership
We would like to reach everyone in the mathematics research community. Please invite a colleague to join the AMR, and feel free to forward this newsletter to colleagues who might be interested. Membership is free and members are kept updated on AMR resources and on opportunities to participate in AMR activities.
Donate
All AMR activities are run by volunteers. We have no paid staff, but we do have a variety of ongoing costs. Please consider donating to help expand our activities and build an organization focused on mathematical research and scholarship. You can donate at amathr.org/donate. The AMR is a is a 501(c)(3) non-profit organization and donations are tax deductible as allowable by law.
Editor: Abigail Thompson
AMR Board of Directors: |
Colin ADAMS, Williams College |
