Reviews
What results from the past have proved unusually influential in current directions of mathematical research? These posts have short reviews of classic mathematical research papers. Most will be about results that appeared in the last half-century.
What are the latest breakthroughs? These posts summarize current mathematical research. They cover significant and influential results announced in talks, preprints, and publications. These results are often preliminary, and their correctness may be as yet uncertain.
These posts examine central open problems, their history, and why their solution would have an impact on progress in mathematics.
Recent Reviews
The Optimal Paper Moebius Band
Author: Sergei Tabachnikov. Everyone knows how to make a Moebius band out of a paper rectangle: give it a $180^{\circ}$ twist and attach the ends to each other. It is easy to do if the rectangle is long and narrow, but it is impossible if the ratio of the length to width is sufficiently small (say, equal to 1). Thus there exists a number $\lambda$ such that if this ratio is greater than $\lambda$, a paper Moebius band can be made, and if it is smaller than $\lambda$, then a paper Moebius band does not exist.
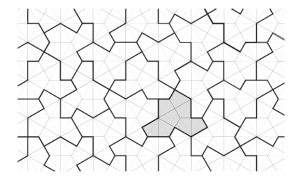
Aperiodic Monotiles
Author: Marjorie Senechal. “A longstanding open problem asks for . . . a shape that admits tilings of the plane, but never periodic tilings. We answer this problem for topological disk tiles by exhibiting a continuum of combinatorially equivalent aperiodic polygons.”
Thus begins the abstract of the preprint “An Aperiodic Monotile,” first posted on arxiv.org on March 20, 2023 by David Smith, Joseph Myers, Craig Kaplan, and Chaim Goodman-Strauss ([1]). Propelled by social media, lively international Zoom gatherings, on-line science magazines, and The New York Times, the news streaked around the globe at (nearly) the speed of light.
Modular invariant q-deformed numbers: first steps
AUTHOR: V. Ovsienko. The goal of this short review is to explain the main ideas of the emerging new theory. of “quantum rational’,’ based on modular, or PSL(2,]-invariance,
and that of “quantum irrationals”.
Ptolemy Relations and Friends
AUTHOR: A. Felikson (Updated 4/4/23): In recent decades, identities similar to the one in Ptolemy’s theorem started to pop up in many fields in connection to the notion of cluster algebras introduced and studied since 2000 by Fomin and Zelevinsky. In this brief note we will try to describe several animals from this big and rich zoo.

Freedman’s Hard Decomposition Theorem
AUTHOR : R. Kirby :EDITORS : J. Hass and R. Ghrist ART : J. Hass INTRODUCTION In his celebrated paper [8], Mike Freedman showed that analogues of

An Aperiodic Set of Eleven Wang Tiles
AUTHORS : B. Durand and A. Shen : EDITOR/ART : R. Ghrist : This is a review of E. Jeandel and M. Rao, “An aperiodic set of
AMR Reviews Scientific Committee
Gil BOR, CIMAT, Mexico ; Anna FELKISON, Durham University, UK; Sergei GELFAND, AMS ; Peter KUCHMENT, Texas A&M University; Vladimir RETAKH, Rutgers University; Sergei TABACHNIKOV, Penn State University