NEW
What are the latest breakthroughs? These posts summarize current mathematical research. They cover significant and influential results announced in talks, preprints and publications. These results are often preliminary, and their correctness may be as yet uncertain.
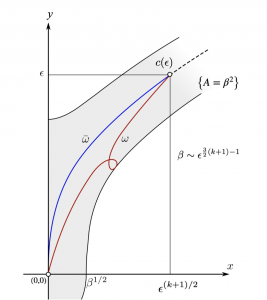
Not all subRiemannian geodesics are smooth
AUTHOR: R. Montgomery. Are all subRiemannian geodesics smooth? The question was answered recently with a decisive “no” by Yacine Chitour, Fr´ederic Jean, Roberto Monti, Ludovic Rifford, Ludovic Sacchelli, Mario Sigalotti, and Alessandro Socionovo.
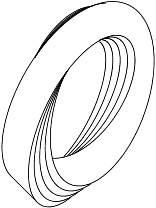
The Optimal Paper Moebius Band
AUTHOR: Sergei Tabachnikov. Everyone knows how to make a Moebius band out of a paper rectangle: give it a $180^{\circ}$ twist and attach the ends to each other. It is easy to do if the rectangle is long and narrow, but it is impossible if the ratio of the length to width is sufficiently small (say, equal to 1). Thus there exists a number $\lambda$ such that if this ratio is greater than $\lambda$, a paper Moebius band can be made, and if it is smaller than $\lambda$, then a paper Moebius band does not exist.
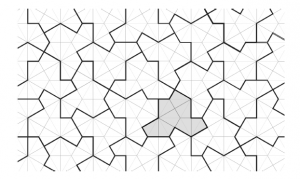
Aperiodic Monotiles
AUTHOR: Marjorie Senechal. “A longstanding open problem asks for . . . a shape that admits tilings of the plane, but never periodic tilings. We answer this problem for topological disk tiles by exhibiting a continuum of combinatorially equivalent aperiodic polygons.”
Thus begins the abstract of the preprint “An Aperiodic Monotile,” first posted on arxiv.org on March 20, 2023 by David Smith, Joseph Myers, Craig Kaplan, and Chaim Goodman-Strauss ([1]). Propelled by social media, lively international Zoom gatherings, on-line science magazines, and The New York Times, the news streaked around the globe at (nearly) the speed of light.
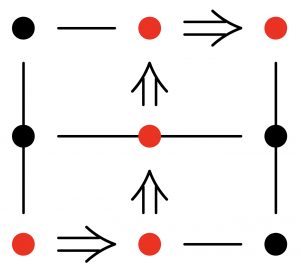
Modular invariant q-deformed numbers: first steps
AUTHOR: V. Ovsienko. The goal of this short review is to explain the main ideas of the emerging new theory. of “quantum rational’,’ based on modular, or PSL(2,]-invariance,
and that of “quantum irrationals”.

Milman and Neeman Post Proof of Triple and Quadruple Bubble Conjectures in $R^n$ and $S^n$
AUTHOR : F. Morgan : EDITORS : J. Hass, R. Ghrist : ART : R. Ghrist In 1884 Hermann Schwarz proved that
Artificial Intelligence in Knot Theory
AUTHOR : C. Adams : EDITOR/ART : R. Ghrist : To move mathematics forward, researchers are constantly seeking new relationships between various areas of

Computability and Undecidability for Euler Fluids
AUTHOR/EDITOR/ART : R. Ghrist : This is a review of recent work by R. Cardona, E. Miranda, D. Peralta-Salas, and F. Presas,

Floating bodies of equilibrium in 2D, the tire track problem, and electrons in a parabolic magnetic field
AUTHOR : S. Tabachnikov : EDITOR/ART : R. Ghrist : This review is for the preprint: F. Wegner, From elastica to floating

The Birkhoff-Poritsky conjecture for centrally-symmetric billiard tables
AUTHOR : S. Tabachnikov : EDITOR/ART : R. Ghrist : This review concerns the following preprint: M. Bialy and A. Mironov, The

