AUTHOR : F. Morgan :
EDITORS : J. Hass, R. Ghrist : ART : R. Ghrist
In 1884 Hermann Schwarz proved that a single round soap bubble is the least-perimeter way to enclose a given volume in $R^3$. In 2000, Michael Hutchings, Frank Morgan, Manual Ritoré, and Antonio Ros proved the Double Bubble Conjecture — that the familiar double soap bubble (see Figure 1) that forms when two soap bubbles come together is the least-perimeter way to enclose and separate two given volumes in $R^3$. Now in 2022 Emanuel Milman and Joe Neeman [MN] have posted a proof of the Triple Bubble Conjecture in all dimensions, and more.


Figure 1. In 2000, Hutchings, Morgan, Ritoré, and Ros proved that the pictured standard double bubble, consisting of three spherical caps meeting at 120 degrees, is the least-perimeter way to enclose and separate two given volumes in $R^3$. Milman and Neeman have recently posted a proof that the pictured standard triple bubble, consisting of spherical caps meeting at 120 degrees along circular arcs, which in turn meet in fours at angles of $\arccos(-1/3) \approx 109^\circ$, is the least-perimeter way to enclose and separate three given volumes in $R^3$, and more.
There is a clear, canonical standard $(n+1)$-bubble in $R^n$, modeled on one in the unit sphere $S^n$. In the easiest case of equal volumes this is just the regular spherical tetrahedron or simplex, with $n+2$ regions in all, including the exterior of the $(n+1)$-bubble, as in Figure 3. The general volumes case in $S^n$ and $R^n$, obtained via conformal mapping, has the same topology, with portions of spheres meeting at the same angles. They extend to higher dimensions by just using the same centers and radii for the portions of spheres, still covering all possible $(n+1)$-tuples of volumes.
Milman and Neeman have now proved the standard triple bubble (as well as the standard double bubble) to be the unique minimizer in $R^n$ and $S^n$ for $n ≥ 3$, the standard quadruple bubble for $n ≥ 4$, and announced the standard quintuple bubble for $n ≥ 5$ (without uniqueness in $R^n$). A month earlier and completely independently, Gary Lawlor announced a proof for the equal-volumes triple bubble in $R^3$. Lawlor’s method is completely different, applying lower-dimensional estimates to slices of competitors.
$R^n$ and $S^n$ apparently require completely new ideas. The 2000 proof by Hutchings et al. of the double bubble conjecture in $R^3$ had three main ingredients:
- Symmetry arguments identified the minimizer as a surface of revolution.
- Hutchings theory [H] bounded the number of components.
- An instability argument ruled out remaining competitors.
The Hutchings bound (2.) is much weaker in higher dimensions and the number of possibilities increases rapidly even for the double bubble. Reichardt managed to carry out (3.) without (2.) to prove the double bubble conjecture in $R^n$, but that seemed to be the limit for that kind of case analysis. (Similar rapid growth in the number of combinatorial possibilities limits the new Milman-Neeman results to triple, quadruple, and quintuple bubbles.) Progress was limited to the few cases when the Hutchings bound limited the double bubble to just two components: when the given volumes were approximately equal.
The new Milman-Neeman proof begins from reflective symmetry, which is all that you get for the triple bubble in $R^3$, for example. The first step uses ingenious families of variations to show that the minimizer consists of pieces of spheres, all centered on the plane of symmetry. This was harder than showing in the Gauss case that the minimizers were flat. It is momentous. For example, in $R^n$ ($n≥3$) it implies the double bubble conjecture from Hutchings’ 1997 relatively easy structure theorem [H], which identifies every nonstandard minimizer as a surface of revolution obtained by adding annular bands to a sphere as in Figure 2. Such bands cannot be spherical.

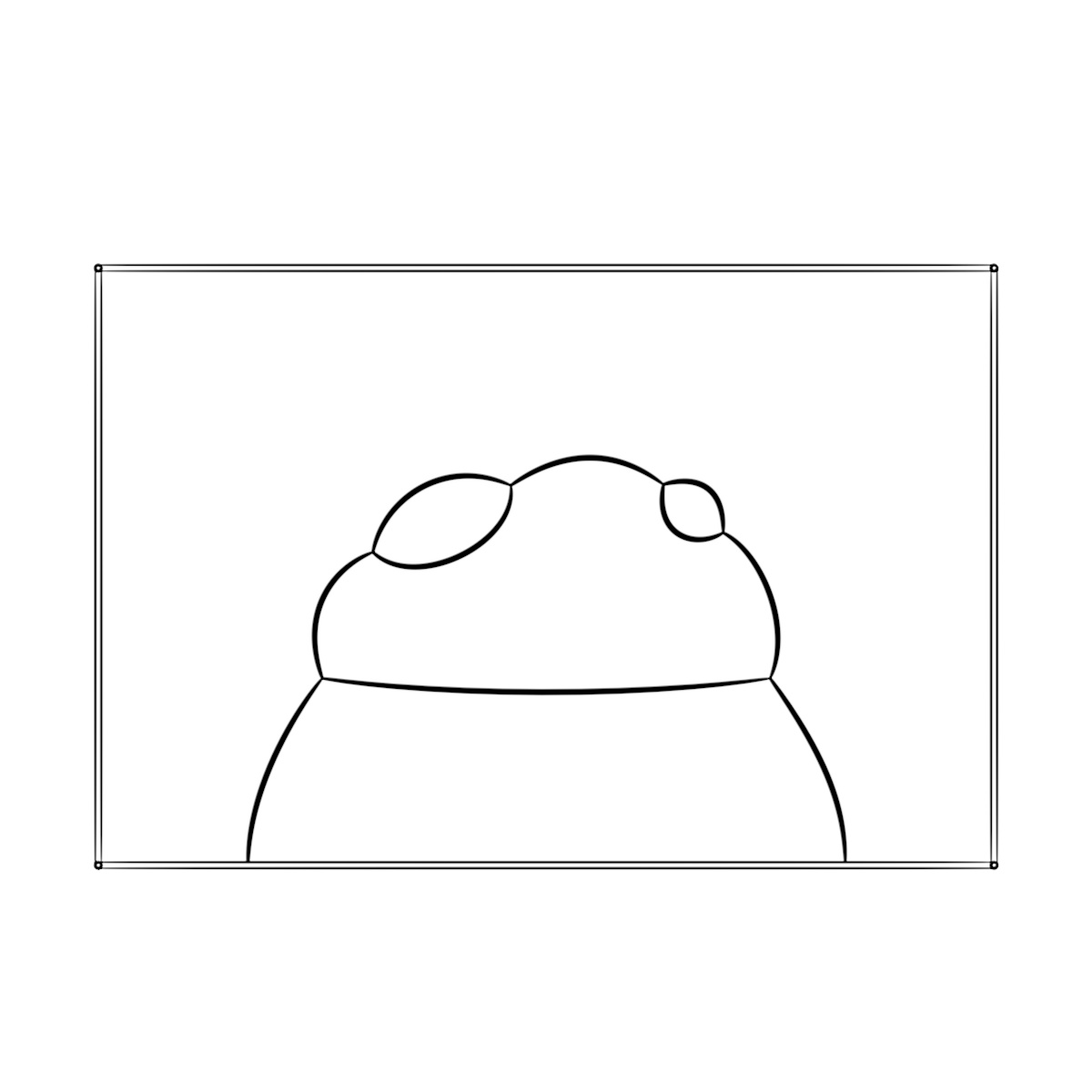
Figure 2. Hutchings’s structure theorem [H] says that a nonstandard area-minimizing double bubble in $R^n$ would be a surface of revolution obtained by adding annular bands to a sphere [left], given as a surface of revolution based on a generating curve [right]. The first step of the Milman and Neeman proof, which proves all bubbles spherical, immediately implies the Double Bubble Conjecture in $R^n$, since such bands cannot be spherical.
The second step gives a certain “Voronoi” structure to the cluster. A particularly nice 3-cluster on $S^2$ as in Figure 3 is the spherical tetrahedron, in which each of the four regions (including the cluster complement) is the set of points closest to one of the four vertices of the dual tetrahedron. This Voronoi structure can be generalized to unequal areas by adding a dependence on the curvatures of the interfaces or the pressures inside the bubbles. The proof moves back and forth between $R^n$ and $S^n$.
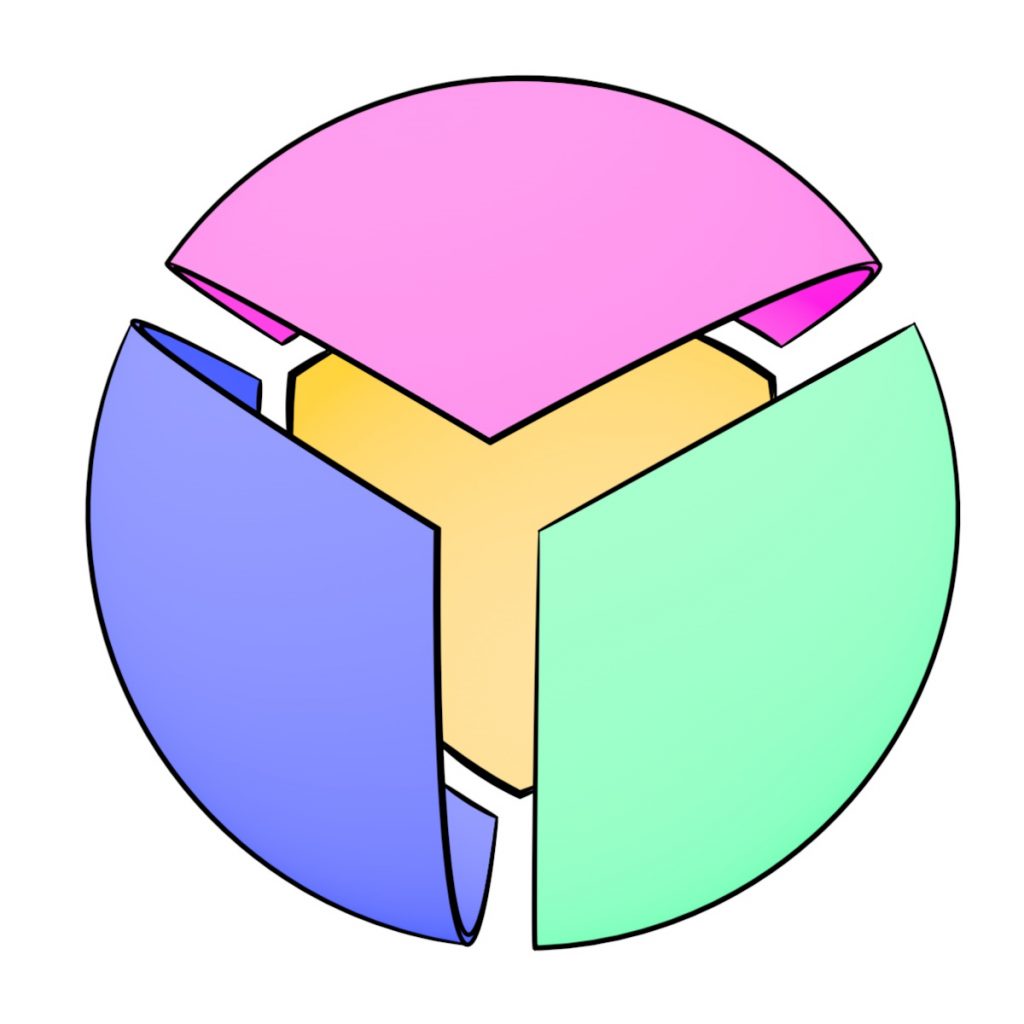
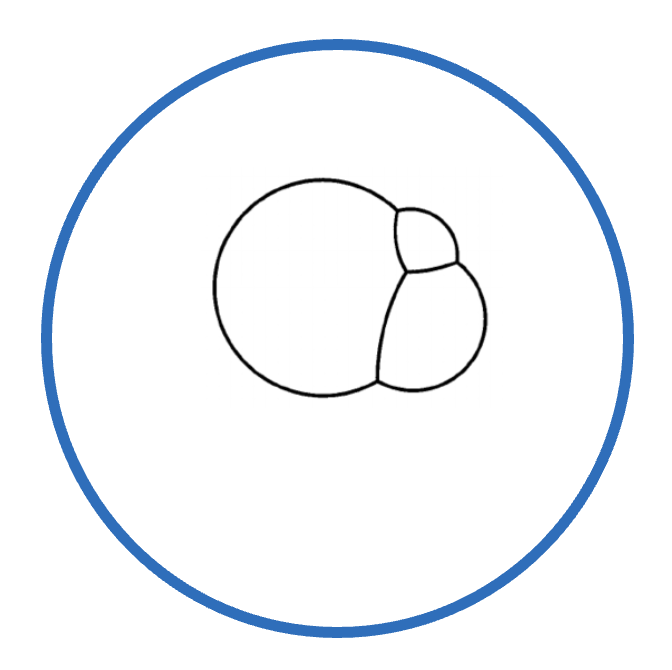
Figure 3. [left] The spherical tetrahedron is the least-perimeter triple bubble on $S^2$: here all three regions and the complement have a quarter of the area. It is a Voronoi partition: each of the four regions is the set of points closest to one of the four vertices of the dual tetrahedron. [right] The Voronoi-like structure can be generalized to unequal areas by adding a dependence on the curvatures of the interfaces or the pressures inside the bubbles.
The third step shows that every region is connected, a great improvement on the Hutchings bound (2). Otherwise the cluster would be unstable under a clever variation, which moves volume from one component of a region to another. The argument is facilitated by first proving that every region intersects the hyperplane of symmetry.
The fourth step shows that every pair of regions is adjacent, ruling out essentially lower-dimensional possibilities, such as a chain of bubbles (an essentially one-dimensional configuration). One lemma rules out a ring of bubbles up through 6-clusters. This step limits the results to 4- or 5-clusters and below.
Throughout there are many daunting technical points, some depending on recent progress in the still incomplete regularity theory.
Open questions and references
Still open are the Quadruple Bubble Conjecture in the Euclidean plane $R^2$ [PT] and the Gaussian plane $G^2$ [C+] and in $R^3$, none with any symmetry in general, and the Double Bubble Conjecture in hyperbolic space $H^3$ [CF]. For more see the Milman-Neeman post itself [MN], with its beautiful explanations, generous remarks, and complete references.
BIBLIOGRAPHY
[C+] Joe Corneli, Ivan Corwin, Stephanie Hurder, Vojislav Sesum, Ya Xu, Elizabeth Adams, Diana Davis, Michelle Lee, Regina Visocchi, and Neil Hoffman, Double bubbles in Gauss space and spheres, Houston J. Math. 34 (2008) 181-204.
[CF] Andrew Cotton and David Freeman, The double bubble problem in spherical space and hyperbolic space, Int. J. Math. Math. Sci. 32 (2002) 641–699.
[H] Michael Hutchings, The structure of area-minimizing double bubbles, J. Geom. Anal. 7 (1997) 285–304.
[MN] Emanuel Milman and Joe Neeman, The structure of isoperimetric bubbles on $R^n$ and $S^n$, https://arxiv.org/abs/2205.09102, May 18, 2022.
[PT] E. Paolini and V. M. Tortorelli, The quadruple planar bubble enclosing equal areas is symmetric, Calc. Var. Partial Differential Equations 59 (2020).
Published Article:
E. Milman, J. Neeman. The structure of isoperimetric bubbles on $R^n$ and $S^n$. Acta Math. 234 (2025), no. 1, 71–188.
Related Videos
Milman on Gaussian Bubbles
Morgan in Oslo on Soap Bubbles and Mathematics
Morgan at Museum of Math
Related Talks
Millman on Multi-Bubble Isoperimetric Problems – Old and New
.

