AUTHOR : S. Tabachnikov :
EDITOR/ART : R. Ghrist :
This review is for the preprint: F. Wegner, From elastica to floating bodies of equilibrium, https://arxiv.org/abs/1909.12596.
Problem No 19 in [14] reads:
Is a solid of uniform density which will float in water in every position a sphere?
This question by S. Ulam can be asked in every dimension; substantial, albeit not yet complete, results are available only in dimension 2.
This flotation problem is closely related with a problem from bicycle kinematics. One models a bicycle as an oriented segment of fixed length that can move in the plane so that the velocity of its rear end is always aligned with the segment: the rear wheel is fixed on the frame, whereas the front wheel can steer. The bicycle leaves two tracks, the front and the rear ones, and usually one can determine the direction of the motion by the geometry tracks, see [6] and the survey [5].
However, sometimes a pair of closed tire tracks, the front and the rear, fail to determine the direction of motion; a trivial example is two concentric circles. Are there other examples?
This “bicycle” problem is equivalent to the 2-dimensional Ulam flotation problem: the front track is the boundary of the floating body, and the rear track is the envelope of the waterline as the body rotates. The ratio of the length of the arc bounded by the waterline to the total length of the boundary is a parameter, and the solutions heavily depend on its value.
For example, the value $1/2$ is easiest to analyze: the solutions comprise an infinite-dimensional space, akin to the curves of constant width, see [1]. In contrast, $1/3$ and $1/4$ are rigid values: a circle is the only solution, see [3,4,7].
A leader in this field is Franz Wegner whose papers mentioned in the title of this review summarize his work on the problem in [9-12] and provide related historical background. Wegner’s web site [13] also surveys his work and offers numerous images and animations, as per the figures below.
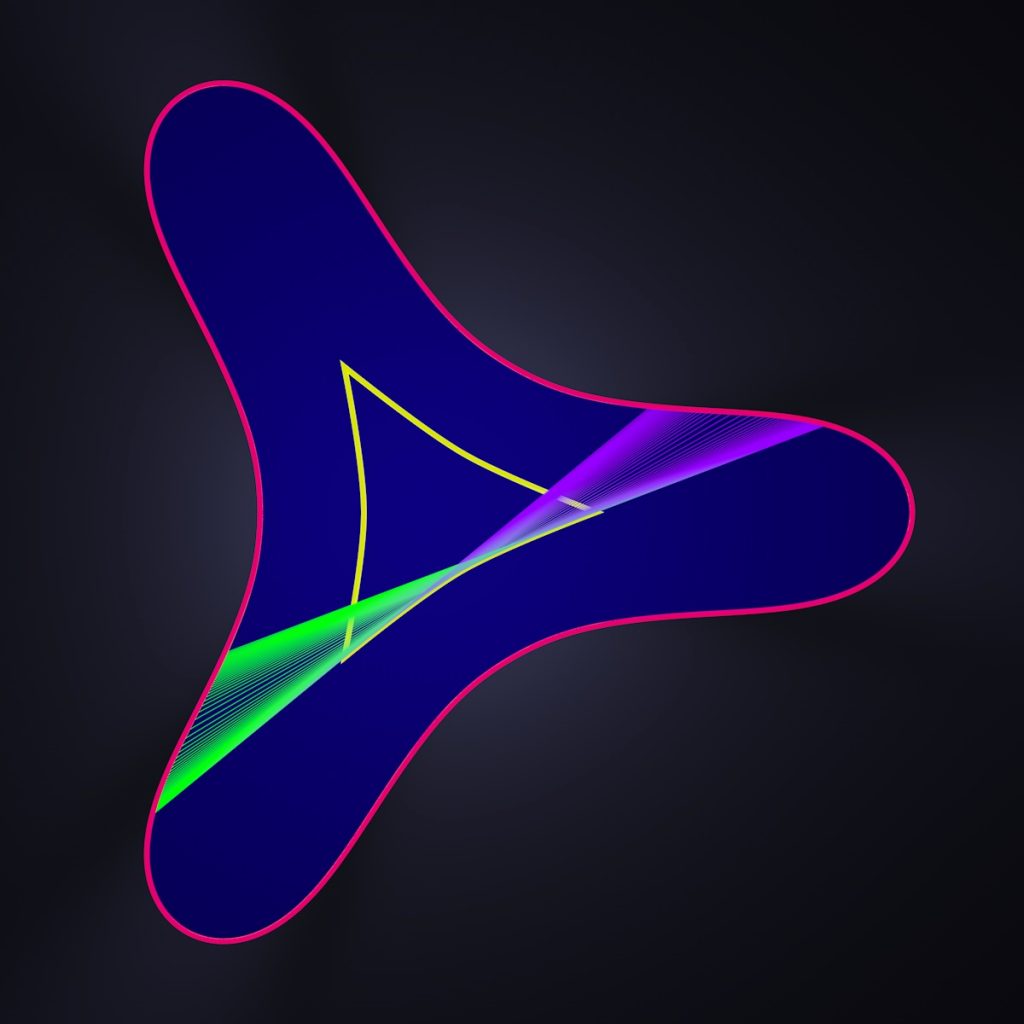


A sampler of Wegner’s solutions: the inner [yellow] curve is the front bicycle track, the outer [pink] curve is the rear track, the purple and green segments tangent to the inner curve are positions of the bicycle moving in the opposite directions. The cusps of the rear track occur when the steering angle reaches $90^{\circ}$ (don’t attempt it in real life!) These solutions enjoy dihedral symmetry. The last curve also solves the problem for the value of the parameter $1/2$. It is a general property of these solutions: the curves having $D_n$-symmetry admit $n-2$ distinct values of the parameter, that come in pairs which sum up to 1, so if $n$ is odd, one of these parameters is $1/2$.
Wegner’s web site [13] is called “Three and more problems — one solution”. Two problems were already mentioned: the flotation in equilibrium and bicycle track problem. The third is the motion of a charge in a magnetic field whose strength is $aR^2+b$, where $R$ is the distance to the origin and $a,b$ are constants. The curvature of the trajectory of the charge equals (up to a constant) the strength of the magnetic field. This yields a differential equation on the curve in polar coordinates which Wegner solved using elliptic functions.

The fourth problem that yields the same solutions is variational: to find closed planar curves that are relative extrema of the bending energy $\int \kappa^2 ds$, where $\kappa$ is the curvature and $s$ the arc length parameter, with the length and area constraints.
Such extremal curves are called buckled rings or pressurized elastica, and they were extensively studied in the late 19th & early 20th century by Halphen, Levy, and Greenhill. The observation that Wegner’s curves are buckled rings was made in [2].
More is true: these curves are solitons of an infinite-dimensional completely integrable system, the planar filament equation $\dot \gamma = \frac{k^2}{2} T + k’ N$, that describes time evolution of a plane curve $\gamma$; here $T$ and $N$ are the unit tangent and normal vectors to the curve, $k$ is its curvature, and $k’$ is the derivative with respect to the length parameter. Solitons are the curves that evolve under the planar filament equation by isometries.
The planar filament equation is a close relative of more physically meaningful filament equation, also known as the smoke ring, binormal, or local induction equation. The filament equation describes evolution of space curves: each point moves in the binormal direction with the speed equal to the curvature, and it is one of the most studied completely integrable systems of soliton type. The filament equation is related to tire track geometry in dimension 3, see [8].
Wegner’s work is a tour de force. He started by considering formal perturbations of the trivial, circular, solution, and found, using a computer algebra system, that an infinitesimal perturbation having $D_n$-symmetry could be extended to several terms of the Taylor expansion, and moreover, that there were $n-2$ different values of the parameter (density) for which the same deformation worked.
This lead to an ansatz, essentially equivalent to the above mentioned differential equation describing the motion of a charge in a magnetic field. Solving this equation made it possible to prove that, for special choices of the parameters, the resulting curves solve the original flotation and bicycle problems.
It is unknown whether Wegner’s solutions are the only solutions to these problems. This is one of many open problems in this area (another open problem concerns a discretization of the previous problems in which smooth curves are replaced by polygons [7]).
BIBLIOGRAPHY
[1] H. Auerbach. Sur un probleme de M. Ulam concernant l’equilibre des corps flottants. Studia Math. 7 (1938), 121–142.
[2] G. Bor, M. Levi, R. Perline, and S. Tabachnikov. Tire tracks and integrable curve evolution. Int. Math. Res. Notes, 2020, no. 9, 2698–2768.
[3] J. Bracho, L. Montejano, and D. Oliveros. A classification theorem for Zindler carrousels. J. Dynam. Control Systems 7 (2001), 367–384.
[4] J. Bracho, L Montejano, and D. Oliveros. Carousels, Zindler curves and the floating body problem. Period. Math. Hungar. 49 (2004), 9–23.
[5] R. Foote, M. Levi, and S. Tabachnikov. Tractrices, bicycle tire tracks, hatchet planimeters, and a 100-year-old conjecture. Amer. Math. Monthly 120 (2013), 199–216.
[6] J. Konhauser, D. Velleman, and S. Wagon. Which Way Did the Bicycle Go?: And Other Intriguing Mathematical Mysteries. Math. Assoc. of America, 1996.
[7] S. Tabachnikov. Tire track geometry: variations on a theme. Israel J. Math. 151 (2006), 1–28.
[8] S. Tabachnikov. On the bicycle transformation and the filament equation: Results and conjectures. J. Geom. Phys., 115 (2017), 116–123.
[9] F. Wegner. Floating bodies of equilibrium. Stud. Appl. Math. 111 (2003), 167–183.
[10] F. Wegner. Floating bodies of equilibrium I. https://arxiv.org/abs/physics/0203061.
[11] F. Wegner. Floating bodies of equilibrium II. https://arxiv.org/abs/physics/0205059.
[12] F. Wegner. Floating bodies of equilibrium. Explicit solution. https://arxiv.org/abs/physics/0603160.
[13] F. Wegner. Three and more problems — one solution. http://www.tphys. uni-heidelberg.de/~wegner/Fl2mvs/Movies.html#float.
[14] The Scottish Book. Mathematics from the Scottish Cafe, with selected problems from the new Scottish Book. Second edition. Ed. by R. Daniel Mauldin. Birkhauser/Springer, Cham, 2015.
All figures (c) 2021 Robert Ghrist.
.
